Вы хотите хорошо сдать ЕГЭ по математике? Тогда вам необходимо уметь считать быстро, правильно и без калькулятора. Ведь главная причина потери баллов на ЕГЭ по математике – вычислительные ошибки.
По правилам проведения ЕГЭ, пользоваться калькулятором на экзамене по математике запрещается. Цена может быть слишком высокой — удаление с экзамена.
На самом деле калькулятор на ЕГЭ по математике не нужен. Все задачи решаются без него. Главное – внимание, аккуратность и некоторые секретные приемы, о которых мы расскажем.
 . Начнем с главного правила. Если какое-то вычисление можно упростить – упростите его.
. Начнем с главного правила. Если какое-то вычисление можно упростить – упростите его.
Вот, например, такое «дьявольское уравнение»:

Семьдесят процентов выпускников решают его «в лоб». Считают дискриминант по формуле , после чего говорят, что корень невозможно извлечь без калькулятора. Но ведь можно разделить левую и правую части уравнения на
, после чего говорят, что корень невозможно извлечь без калькулятора. Но ведь можно разделить левую и правую части уравнения на  . Получится
. Получится

Какой способ проще? :-)
 . Многие школьники не любят умножение в «столбик». Никому не нравилось в четвертом классе решать скучные «примеры». Однако перемножить числа во многих случаях можно и без «столбика», в строчку. Это намного быстрее.
. Многие школьники не любят умножение в «столбик». Никому не нравилось в четвертом классе решать скучные «примеры». Однако перемножить числа во многих случаях можно и без «столбика», в строчку. Это намного быстрее.


Обратите внимание, что мы начинаем не с меньших разрядов, а с бoльших. Это удобно.
 . Теперь – деление. Нелегко «в столбик» разделить
. Теперь – деление. Нелегко «в столбик» разделить  на
на  . Но вспомним, что знак деления : и дробная черта – одно и то же. Запишем
. Но вспомним, что знак деления : и дробная черта – одно и то же. Запишем  в виде дроби и сократим дробь:
в виде дроби и сократим дробь:

Другой пример.
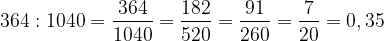
 . Как быстро и без всяких столбиков возвести в квадрат двузначное число? Применяем формулы сокращенного умножения:
. Как быстро и без всяких столбиков возвести в квадрат двузначное число? Применяем формулы сокращенного умножения:




Иногда удобно использовать и другую формулу:



 . Числа, оканчивающиеся на
. Числа, оканчивающиеся на 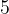 , в квадрат возводятся моментально.
, в квадрат возводятся моментально.
Допустим, надо найти квадрат числа (
( — не обязательно цифра, любое натуральное число). Умножаем
— не обязательно цифра, любое натуральное число). Умножаем  на
на  и к результату приписываем
и к результату приписываем  . Всё!
. Всё!
Например: (
( и приписали
и приписали  ).
).
 (
( и приписали
и приписали  ).
).
 (
( и приписали
и приписали  ).
).
Этот способ полезен не только для возведения в квадрат, но для извлечения квадратного корня из чисел, оканчивающихся на .
.
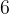 . А как вообще извлечь квадратный корень без калькулятора? Покажем два способа.
. А как вообще извлечь квадратный корень без калькулятора? Покажем два способа.
Первый способ – разложение подкоренного выражения на множители.
Например, найдем
Число делится на
делится на 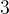 (так как сумма его цифр делится на
(так как сумма его цифр делится на 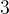 ). Разложим
). Разложим  на множители:
на множители:


Найдем . Это число делится на
. Это число делится на  . На
. На 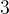 оно тоже делится. Раскладываем
оно тоже делится. Раскладываем  на множители.
на множители.

Еще пример.

Есть и второй способ. Он удобен, если число, из которого надо извлечь корень, никак не получается разложить на множители.
Например, надо найти . Число под корнем – нечетное, оно не делится на
. Число под корнем – нечетное, оно не делится на 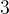 , не делится на
, не делится на 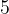 , не делится на
, не делится на  … Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.
… Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.
Очевидно, что в квадрат возводили двузначное число, которое находится между числами и
и  , поскольку
, поскольку  ,
,  , а число
, а число  находится между ними. Первую цифру в ответе мы уже знаем, это
находится между ними. Первую цифру в ответе мы уже знаем, это  .
.
Последняя цифра в числе равна
равна  . Поскольку
. Поскольку  ,
, 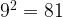 , последняя цифра в ответе – либо
, последняя цифра в ответе – либо  , либо
, либо  . Проверим:
. Проверим:
 . Получилось!
. Получилось!
Найдем .
.
 ,
,  . Значит, первая цифра в ответе – пятерка.
. Значит, первая цифра в ответе – пятерка.
В числе последняя цифра – девятка.
последняя цифра – девятка. 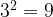 ,
,  . Значит, последняя цифра в ответе – либо
. Значит, последняя цифра в ответе – либо 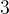 , либо
, либо  .
.
Проверим:

Если число, из которого надо извлечь квадратный корень, заканчивается на или
или  – значит, квадратный корень из него будет числом иррациональным. Потому что ни один квадрат целого числа не заканчивается на
– значит, квадратный корень из него будет числом иррациональным. Потому что ни один квадрат целого числа не заканчивается на  или
или  . Помните, что в задачах части
. Помните, что в задачах части  вариантов ЕГЭ по математике ответ должен быть записан в виде целого числа или конечной десятичной дроби, то есть должен являться рациональным числом.
вариантов ЕГЭ по математике ответ должен быть записан в виде целого числа или конечной десятичной дроби, то есть должен являться рациональным числом.
 . Квадратные уравнения встречаются нам в задачах
. Квадратные уравнения встречаются нам в задачах  ,
, 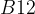 и
и 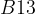 вариантов ЕГЭ, а также в части
вариантов ЕГЭ, а также в части  . В них нужно считать дискриминант, а затем извлекать из него корень. И совсем не обязательно искать корни из пятизначных чисел. Во многих случаях дискриминант удается разложить на множители.
. В них нужно считать дискриминант, а затем извлекать из него корень. И совсем не обязательно искать корни из пятизначных чисел. Во многих случаях дискриминант удается разложить на множители.
Например, в уравнении
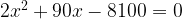


 . Иногда дискриминант удается посчитать по известной формуле сокращенного умножения:
. Иногда дискриминант удается посчитать по известной формуле сокращенного умножения: 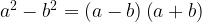 . Вот, например, такое уравнение вполне может получиться при решении задачи
. Вот, например, такое уравнение вполне может получиться при решении задачи 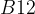 :
:
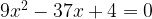


 . Еще одна ситуация, в которой выражение под корнем можно разложить на множители, взята из задачи
. Еще одна ситуация, в которой выражение под корнем можно разложить на множители, взята из задачи  .
.
Гипотенуза прямоугольного треугольника равна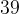 , один из катетов равен
, один из катетов равен 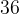 , найти второй катет.
, найти второй катет.
По теореме Пифагора, он равен . Можно долго считать в столбик, но проще применить формулу сокращенного умножения.
. Можно долго считать в столбик, но проще применить формулу сокращенного умножения.


А теперь расскажем самое интересное — из-за чего все-таки выпускники теряют на ЕГЭ драгоценные баллы. Ведь ошибки в вычислениях возникают не просто так.
 1. Верный путь к потере баллов — неаккуратные вычисления, в которых что-то исправлено, зачеркнуто, одна цифра написана поверх другой. Посмотрите на свои черновики. Возможно, они выглядят так же? :-)
1. Верный путь к потере баллов — неаккуратные вычисления, в которых что-то исправлено, зачеркнуто, одна цифра написана поверх другой. Посмотрите на свои черновики. Возможно, они выглядят так же? :-)
Пишите разборчиво! Не экономьте бумагу. Если что-то неправильно – не исправляйте одну цифру на другую, лучше напишите заново.
2. Почему-то многие школьники, считая в столбик, стараются сделать это 1) очень-очень быстро, 2) очень мелкими цифрами, в уголке тетради и 3) карандашом. В результате получается вот что:



Разобрать что-либо невозможно. Что ж тогда удивляться, что оценка за ЕГЭ ниже, чем ожидали?
3. Многие школьники привыкли игнорировать скобки в выражениях. Иногда встречается и такое:
 Помните, что знак равенства ставится не где попало, а только между равными величинами. Пишите грамотно, даже на черновике.
Помните, что знак равенства ставится не где попало, а только между равными величинами. Пишите грамотно, даже на черновике.
 4. Огромное количество вычислительных ошибок связано с дробями. Если вы делите дробь на дробь – пользуйтесь тем, что
4. Огромное количество вычислительных ошибок связано с дробями. Если вы делите дробь на дробь – пользуйтесь тем, что 
Здесь нарисован «гамбургер», то есть многоэтажная дробь. Крайне сложно при таком способе получить правильный ответ.
Подведем итоги.
Проверка заданий части – автоматическая. Здесь не бывает «почти правильного» ответа. Либо он правилен, либо нет. Одна вычислительная ошибка – и привет, задача не засчитывается. Поэтому в ваших интересах научиться считать быстро, правильно и без калькулятора.
– автоматическая. Здесь не бывает «почти правильного» ответа. Либо он правилен, либо нет. Одна вычислительная ошибка – и привет, задача не засчитывается. Поэтому в ваших интересах научиться считать быстро, правильно и без калькулятора.
Задания части проверяет эксперт. Позаботьтесь о нем! Пусть ему будет понятен и ваш почерк, и логика решения.
проверяет эксперт. Позаботьтесь о нем! Пусть ему будет понятен и ваш почерк, и логика решения.
Самое главное – ваши вычисления должны быть максимально простыми. Есть известный принцип, применяемый в программировании и дизайне. По-английски он звучит так: «Keep it simple, stupid!» и легко запоминается как KISS :-)
По правилам проведения ЕГЭ, пользоваться калькулятором на экзамене по математике запрещается. Цена может быть слишком высокой — удаление с экзамена.
На самом деле калькулятор на ЕГЭ по математике не нужен. Все задачи решаются без него. Главное – внимание, аккуратность и некоторые секретные приемы, о которых мы расскажем.
Вот, например, такое «дьявольское уравнение»:
Семьдесят процентов выпускников решают его «в лоб». Считают дискриминант по формуле
Какой способ проще? :-)
Обратите внимание, что мы начинаем не с меньших разрядов, а с бoльших. Это удобно.
Другой пример.
Иногда удобно использовать и другую формулу:
Допустим, надо найти квадрат числа
Например:
Этот способ полезен не только для возведения в квадрат, но для извлечения квадратного корня из чисел, оканчивающихся на
Первый способ – разложение подкоренного выражения на множители.
Например, найдем
Число
Найдем
Еще пример.
Есть и второй способ. Он удобен, если число, из которого надо извлечь корень, никак не получается разложить на множители.
Например, надо найти
Очевидно, что в квадрат возводили двузначное число, которое находится между числами
Последняя цифра в числе
Найдем
В числе
Проверим:
Если число, из которого надо извлечь квадратный корень, заканчивается на
Например, в уравнении
Гипотенуза прямоугольного треугольника равна
По теореме Пифагора, он равен
А теперь расскажем самое интересное — из-за чего все-таки выпускники теряют на ЕГЭ драгоценные баллы. Ведь ошибки в вычислениях возникают не просто так.
 1. Верный путь к потере баллов — неаккуратные вычисления, в которых что-то исправлено, зачеркнуто, одна цифра написана поверх другой. Посмотрите на свои черновики. Возможно, они выглядят так же? :-)
1. Верный путь к потере баллов — неаккуратные вычисления, в которых что-то исправлено, зачеркнуто, одна цифра написана поверх другой. Посмотрите на свои черновики. Возможно, они выглядят так же? :-)Пишите разборчиво! Не экономьте бумагу. Если что-то неправильно – не исправляйте одну цифру на другую, лучше напишите заново.
2. Почему-то многие школьники, считая в столбик, стараются сделать это 1) очень-очень быстро, 2) очень мелкими цифрами, в уголке тетради и 3) карандашом. В результате получается вот что:



Разобрать что-либо невозможно. Что ж тогда удивляться, что оценка за ЕГЭ ниже, чем ожидали?
3. Многие школьники привыкли игнорировать скобки в выражениях. Иногда встречается и такое:
 Помните, что знак равенства ставится не где попало, а только между равными величинами. Пишите грамотно, даже на черновике.
Помните, что знак равенства ставится не где попало, а только между равными величинами. Пишите грамотно, даже на черновике. 4. Огромное количество вычислительных ошибок связано с дробями. Если вы делите дробь на дробь – пользуйтесь тем, что
4. Огромное количество вычислительных ошибок связано с дробями. Если вы делите дробь на дробь – пользуйтесь тем, что Здесь нарисован «гамбургер», то есть многоэтажная дробь. Крайне сложно при таком способе получить правильный ответ.
Подведем итоги.
Проверка заданий части
Задания части
Самое главное – ваши вычисления должны быть максимально простыми. Есть известный принцип, применяемый в программировании и дизайне. По-английски он звучит так: «Keep it simple, stupid!» и легко запоминается как KISS :-)
Комментариев нет:
Отправить комментарий